Distributions

library(torch)
torch_manual_seed(1) # setting seed for reproducibility

This vignette showcases the basic functionality of distributions in torch. Currently the distributions modules are considered ‘work in progress’ and are still experimental features in the torch package. You can see the progress in this link.

The distributions modules in torch are modelled after PyTorch’s distributions module which in turn is based on the TensorFlow Distributions package.

This vignette is based in the TensorFlow’s distributions tutorial.

Basic univariate distributions

Let’s start and create a new instance of a normal distribution:

n <- distr_normal(loc = 0, scale = 1)
n
#> torch_Normal ()

We can draw samples from it with:

n$sample()
#> torch_tensor
#>  0.6614
#> [ CPUFloatType{1} ]

or, draw multiple samples:

n$sample(3)
#> torch_tensor
#>  0.2669
#>  0.0617
#>  0.6213
#> [ CPUFloatType{3,1} ]

We can evaluate the log probability of values:

n$log_prob(0)
#> torch_tensor
#> -0.9189
#> [ CPUFloatType{1} ]

log(dnorm(0)) # equivalent R code
#> [1] -0.9189385

or, evaluate multiple log probabilities:

n$log_prob(c(0, 2, 4))
#> torch_tensor
#> -0.9189
#> -2.9189
#> -8.9189
#> [ CPUFloatType{3} ]

Multiple distributions

A distribution can take a tensor as it’s parameters:

b <- distr_bernoulli(probs = torch_tensor(c(0.25, 0.5, 0.75)))
b
#> torch_Bernoulli ()

This object represents 3 independent Bernoulli distributions, one for each element of the tensor.

We can sample a single observation:

b$sample()
#> torch_tensor
#>  0
#>  1
#>  1
#> [ CPUFloatType{3} ]

or, a batch of n observations:

b$sample(6)
#> torch_tensor
#>  0  0  1
#>  0  1  1
#>  0  0  1
#>  0  1  1
#>  0  1  1
#>  0  0  1
#> [ CPUFloatType{6,3} ]

Using distributions within models

The log_prob method of distributions can be differentiated, thus, distributions can be used to train models in torch.

Let’s implement a Gaussian linear model, but first let’s simulate some data

x <- torch_randn(100, 1)
y <- 2*x + 1 + torch_randn(100, 1)

and plot:

plot(as.numeric(x), as.numeric(y))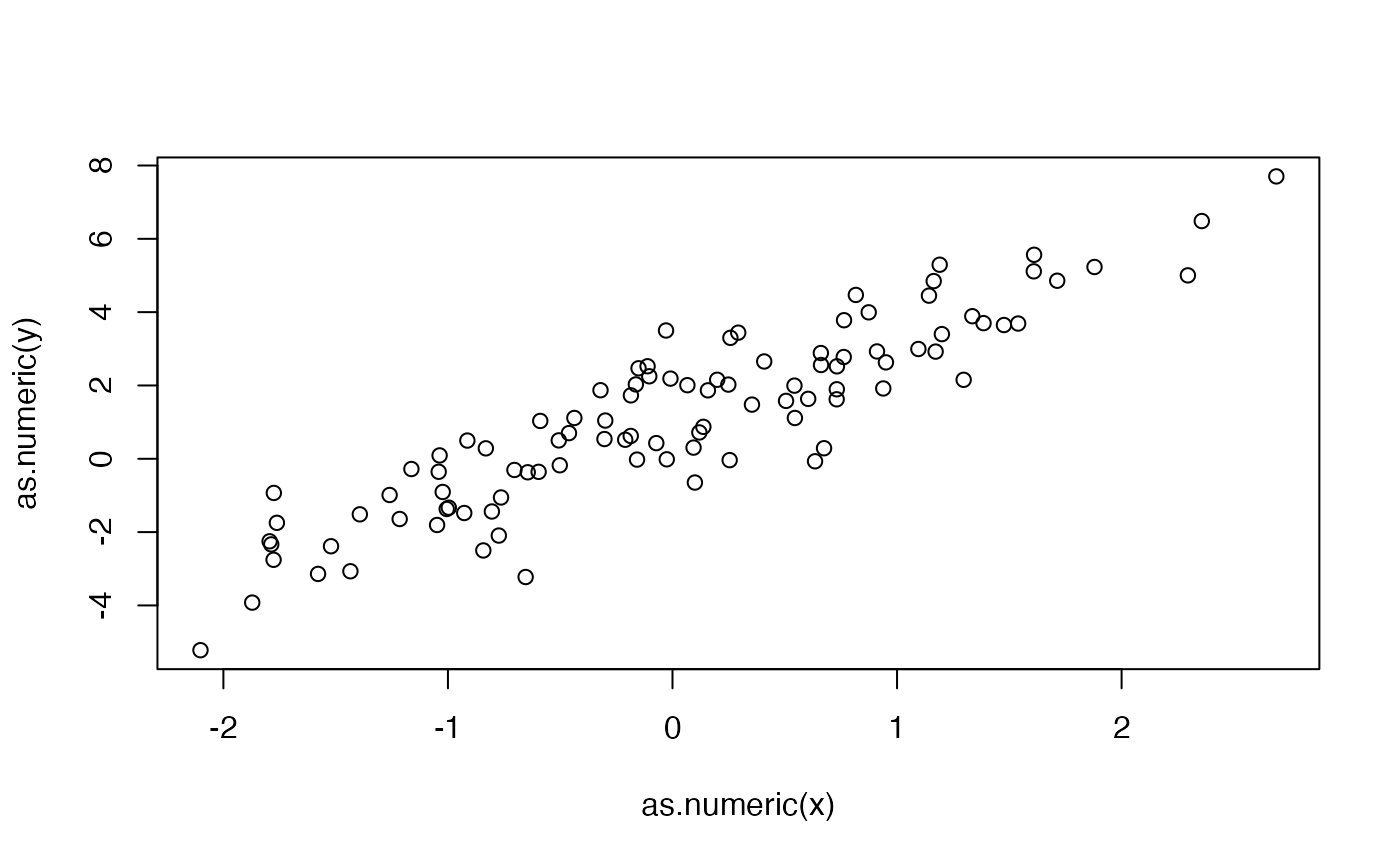

We can now define our model:

GaussianLinear <- nn_module(
  initialize = function() {
    # this linear predictor will estimate the mean of the normal distribution
    self$linear <- nn_linear(1, 1)
    # this parameter will hold the estimate of the variability
    self$scale <- nn_parameter(torch_ones(1))
  },
  forward = function(x) {
    # we estimate the mean
    loc <- self$linear(x)
    # return a normal distribution
    distr_normal(loc, self$scale)
  }
)

model <- GaussianLinear()

We can now train our model with:

opt <- optim_sgd(model$parameters, lr = 0.1)

for (i in 1:100) {
  opt$zero_grad()
  d <- model(x)
  loss <- torch_mean(-d$log_prob(y))
  loss$backward()
  opt$step()
  if (i %% 10 == 0)
    cat("iter: ", i, " loss: ", loss$item(), "\n")
}
#> iter:  10  loss:  1.975726 
#> iter:  20  loss:  1.790831 
#> iter:  30  loss:  1.64495 
#> iter:  40  loss:  1.532009 
#> iter:  50  loss:  1.478054 
#> iter:  60  loss:  1.465937 
#> iter:  70  loss:  1.464229 
#> iter:  80  loss:  1.464002 
#> iter:  90  loss:  1.463971 
#> iter:  100  loss:  1.463966

We can see the parameter estimates with:

model$parameters
#> $linear.weight
#> torch_tensor
#>  2.1256
#> [ CPUFloatType{1,1} ][ requires_grad = TRUE ]
#> 
#> $linear.bias
#> torch_tensor
#>  1.1215
#> [ CPUFloatType{1} ][ requires_grad = TRUE ]
#> 
#> $scale
#> torch_tensor
#>  1.0461
#> [ CPUFloatType{1} ][ requires_grad = TRUE ]

and quickly compare with the glm() function:

summary(glm(as.numeric(y) ~ as.numeric(x)))
#> 
#> Call:
#> glm(formula = as.numeric(y) ~ as.numeric(x))
#> 
#> Coefficients:
#>               Estimate Std. Error t value Pr(>|t|)    
#> (Intercept)     1.1226     0.1057   10.62   <2e-16 ***
#> as.numeric(x)   2.1259     0.1009   21.08   <2e-16 ***
#> ---
#> Signif. codes:  0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1
#> 
#> (Dispersion parameter for gaussian family taken to be 1.116565)
#> 
#>     Null deviance: 605.56  on 99  degrees of freedom
#> Residual deviance: 109.42  on 98  degrees of freedom
#> AIC: 298.79
#> 
#> Number of Fisher Scoring iterations: 2